In this article, I’m gonna speak a little about interpolation. And why we mostly choose an interpolation scheme rather than another. So, as you would have guessed, the topic will be about mathematics in the first part and animation on second one (jump straight to animation if you do not care, but I promise, even the first part is easy to understand and really valuable!)
About Interpolation
A link between continuous and discrete representation
Let’s say I have a curve. A curve is continuous: you can draw it without lifting your hand. However, when we are doing animation, we do not consider the time as continuous anymore, we represent it as ‘keyframes’. If we want to represent how we moved on the curve, we would just put points at some places: a point means ‘I was here at that frame’. Representing something continuous as a countable number of points is called a ‘discrete’ representation

So, as we can see, it is pretty easy to go from continous to discrete, we just have to put points at the exat moment. In animation, even though the motion is supposed to be contiuous, we can represent it by still frames and the illusion of movement works if the framerate is high enough. So, in a way, animation is just a discretization of the movement
However, what if I give you points and ask you to draw the original curve? The question is way more complicated and sometimes impossible to do if there is not enough points, or if they are not distributed well enough.

Of course, it is impossible to find exactly the initial curve, we can always lose some level of details. But we can still hope to find something that is really similar to our initial curve. This process of approximating a continuous curve using a discrete representation of it (i.e points from the curve) is called INTERPOLATION.
OK, but how do we do that?
Note: for hands-on examples, go check the notebook I made especially for this topic: here
The first idea to solve this problem is fairly simple: let’s say I have points that are supposed to make a curve, how can I recreate that curve? Basic answer is: I just need to draw a line between each consecutive points. And that’s exactly what linear interpolation is!
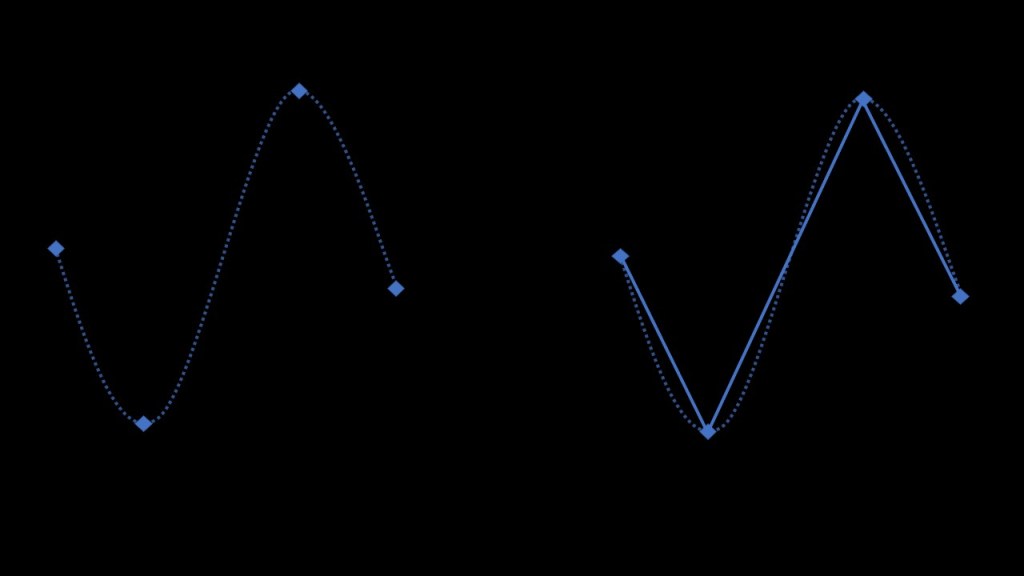
As you may notice, given that we have enough points, the result is pretty good as it approximates well the initial curve. The more point we have, the closer we will be. But there is a huge problem. The curve that we constructed (the consecutive lines) is not smooth! It looks somehow geometric and not fairly natural. For multiple reasons (that I will cover in next section) we do not like that at all and want to avoid this non-smoothness! To do so we use ‘spline’ type interpolations (there are multiple sorts of splines) that allows us to recreate a smooth approximation of the curve!

About why spline is better than linear (in most cases)
Let’s talk physics
To understand what’s the point, we need some really basic notions of physics. Animation is all about physics after all!
In physics, when considering the movement of a point, we introduce two values that we find pretty valuable: speed and acceleration. Speed is how fast our point moves and the acceleration is ‘the speed of the speed’ i.e a positive acceleration means that the speed goes up so our point moves faster and faster, negative acceleration means the speed goes down so our points moves slower and slower.
On a graph representing, for example, the value of Translate Y of our point, we can read the speed quite easily. The speed is just the slope of our curve!



Let’s analyze a linearly interpolated curve with that perspective
So let’s just draw a linear interpolation and check what is the speed of our point!


You may notice something unusual: the speed is not continuous!!! Indeed, the slope brutally changes on each point we interpolated!
What is a discontinuity in the speed? It means that there is an infinite acceleration at that moment! And guess what? Infinite acceleration almost never occur in real life. In certain situations it can be acceptable (e.g robotic motion or bounces of a rigid body) as it is close to the phenomena, but most of the time it will not work and will result in an awkward feeling of the motion!
However, when using spline type interpolation, the result is smooth, and it is much better: we don’t have those discontinuities anymore!


In summary
- Linear interpolation: it means constant speed! So if you need something that goes at a constant speed (robotic arm or elevator or such, why not!). But take care of tangent breaks!
- Spline interpolation: smooth way to interpolate! It will make the transition smoother so that you will start to have an ‘ease-out’ and an ‘ease-in’! BUT rework your dynamics by yourself as the interpolation will not make it perfect!